
Meetkundige uitleg over de structuur van de levensboom.
Een fractal is een meetkundige figuur met ingebouwde zelf-gelijkvormigheid, herhaling van hetzelfde patroon op steeds kleinere schaal.
Hij groeit op basis van de rechthoekige driehoek 1 -2 -wortel(5).
Een bijzondere eigenschap is de volgende:
We stellen dat het eerste vierkant de afmetingen 1 bij 1 heeft.
Als je dan de oppervlakte van alle delen bij elkaar optelt, tot zelfs de allerkleinste ( de nog onzichtbare) aan toe, dan is die oppervlakte totaal exact gelijk aan 3.
Een geheel getal, hoe is het mogelijk?!
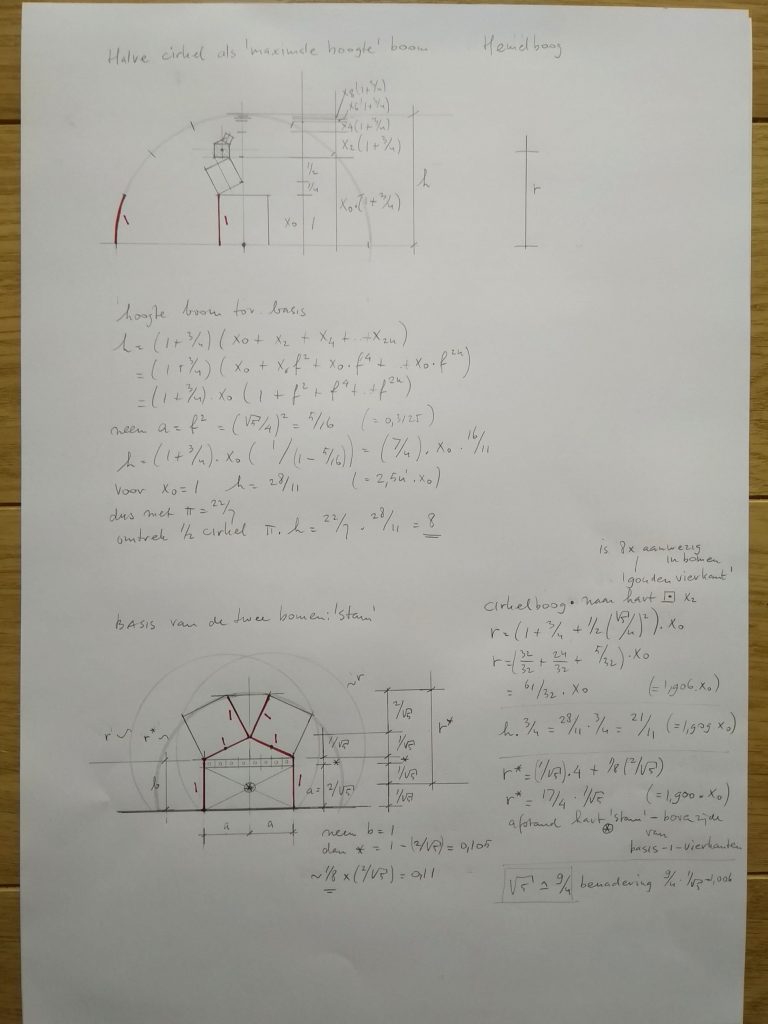
Nog wat bijzonderheden van deze boom.
Je kunt bij een fractal ook de maximale hoogte van de boom bepalen, tot aan de allerkleinste delen aan toe, hier zijnde 28/11.
Nu rekende men vroeger altijd in breuken
(niet decimaal, met vele cijfers achter de komma)
en de waarde voor de verhouding ‘pi’ is 22/7.
En dat is een heel goede benadering voor ‘onze’ ‘pi’.
Dus daaruit volgt dat de omtrek van deze boom (halve cirkelboog) gelijk is aan 28/11 * 22/7 = 8.
Weer een geheel getal, wonderbaarlijk toch?