Dit is het dilemma.
Om de omtrek van de cirkel te bepalen, moet je kiezen tussen een hoekverdeling
in graden óf in radialen.
De keuze voor de verdeling bij de klok ( 12) en de gradenboog (360) ( als bij de rode GESLOTEN cirkel, met omtrek 24) is feitelijk gebaseerd op het begrip graden in de goniometrie.
De eenheid van een hoek is graad, met 360 graden in een volledige cirkel.
Een goede keuze, want de waarde 360 is eenvoudig deelbaar door 12 en ook door 2, 3, 4, 5, 6, 8, 9, 10 enzovoort.
Het alternatief (de zwarte OPEN cirkelboog) is dat we kiezen voor radialen.
De eenheid voor een hoek is radiaal, met 2 Pi radialen in een volledige eenheidscirkel.
De breukwaarde van Pi is 22/ 7, dus gelijk aan 3 + 1 /7.
Pi is gebaseerd op ‘het aantal keren dat de straal 1 langs de omtrek van de eenheidscirkel kan worden afgemeten’. In de eenheidscirkel is de straal is 1 en de diameter dus gelijk aan 2.
En een goede keuze voor afmeting van de diameter
is een heel praktisch uitgangspunt.
Elk ‘weefsel’ helpt ons om tijd en/of plaats vast te leggen in eenvoudige en begrijpelijke stappen.
Er zijn duidelijk twee verschillende uitgangspunten.
De gesloten cirkel en de open cirkelboog hebben allebei hun goede kanten. Ze zullen naast elkaar blijven bestaan.
Het is juist dit verschil tussen Pi en 3 ( circa 1/7 groot) waar de oplossing gevonden kan worden.
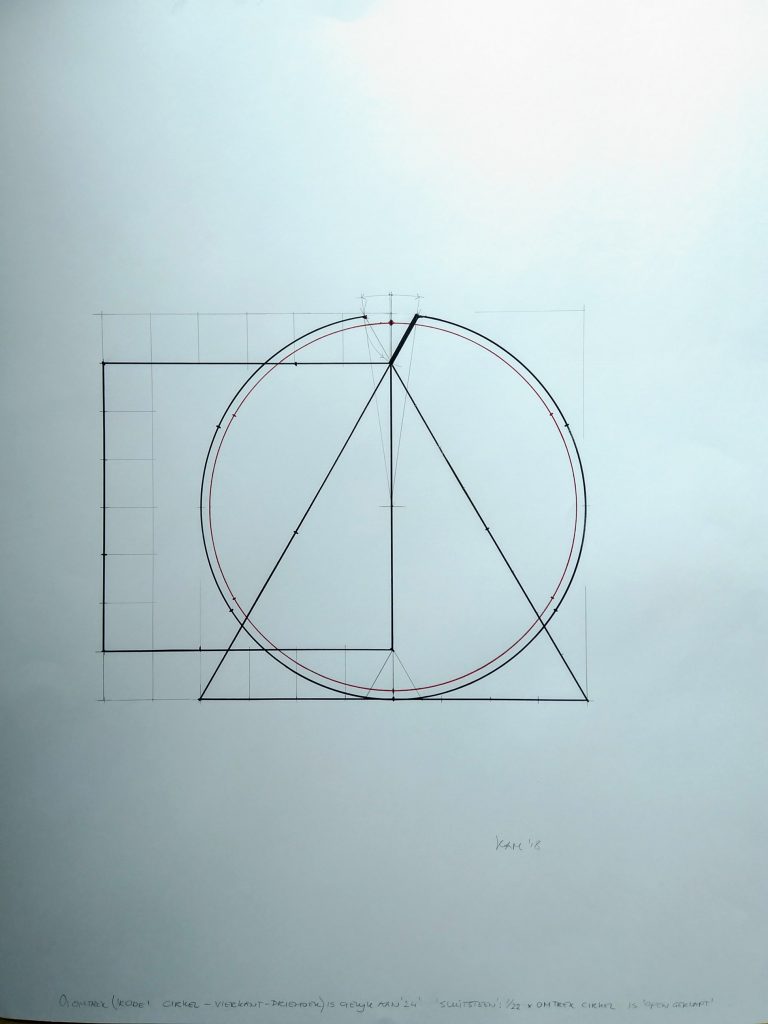
Op basis van graden
We gaan op basis van 1.Koningen ( graden) de omtrek berekenen.
Onze aanname is
– Omtrek rode gesloten cirkel is 3 * 8 = 24 ( naar Salomo)
‘diameter’ is gelijk aan 8 ( ongeacht de maateenheid/ meters/ ellen)
– Omtrek blauwe driehoek is 24 , dus zijde 24 / 3 = 8
– Omtrek gele vierkant is 24, dus zijde is 24 / 4= 6
Verder nemen we eenvoudig aan voor
Pi : breuk 22/ 7
Wortel (3) : breuk 7/ 4
Dus bij driehoek is verhouding hoogte/ breedte gelijk aan: 7 /8
Omtrek van zwarte open cirkelboog is 24, ‘resterende’ opening aan de bovenzijde is
(Pi – 3) * 8 = (( 22 / 7) – 3 ) * 8 = ( 1/ 7) * 8 = 8/ 7
‘Hé, die laatste maat is jammer genoeg geen geheel getal…‘
Zie hieronder het resultaat, de geometrie waarbij de drie basisfiguren met elkaar worden verweven:
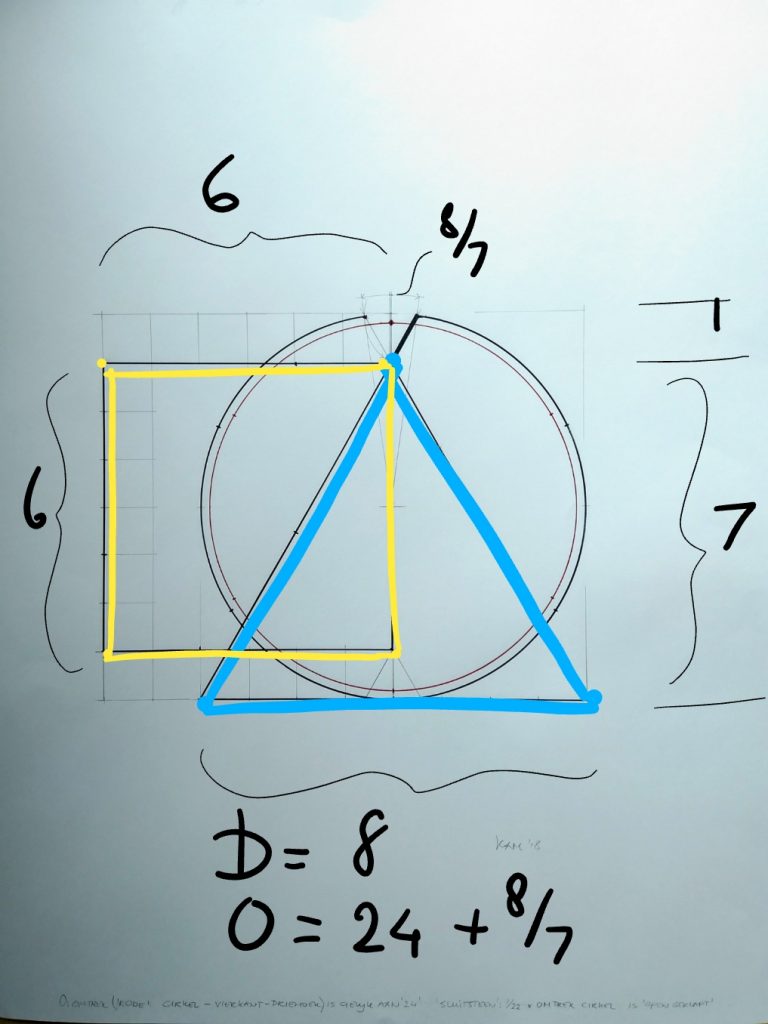
Op basis van radialen
De oplossing uitgaande van radialen en verhoudingsgetal ‘Pi’.
Circa 250 voor Christus stelde de geleerde Archimedes
dat ‘Pi’ goed kan worden benaderd door de breuk 22/ 7.
Onze gunstige aanname is een diameter gelijk aan 7 ( ongeacht de maateenheid/ meters/ ellen) .
Omtrek rode cirkel is 3 * 7 = 21 ( naar Salomo)
Omtrek blauwe driehoek is 21 , dus zijde 21 / 3 = 7
Omtrek gele vierkant is 21, dus zijde is 21 / 4
‘Hé, die laatste maat is jammer genoeg geen geheel getal…‘
Omtrek van de zwarte cirkel is Pi * 7 = ( 22 / 7 ) * 7 = 22
De opening aan de bovenzijde bedraagt ( Pi -3 ) * 7 = 22 – 21 = 1
‘Ha, dat is wel mooier dan bij de eerste oplossing: (8/7)‘
Hieruit volgt:
De verhouding tussen de
opening : volledige omtrek zwarte cirkel = 1 : 22
Dit is de tekst van Lucas 3, 21 en 22 ( eigenlijk best wel opvallende getallen in deze) over Jezus’ Doop in de Jordaan
Verder nemen we eenvoudig aan voor
Pi : breuk 22/ 7
Wortel (3) : breuk 7/ 4
Dus bij driehoek is verhouding hoogte/ breedte gelijk aan: 7 /8

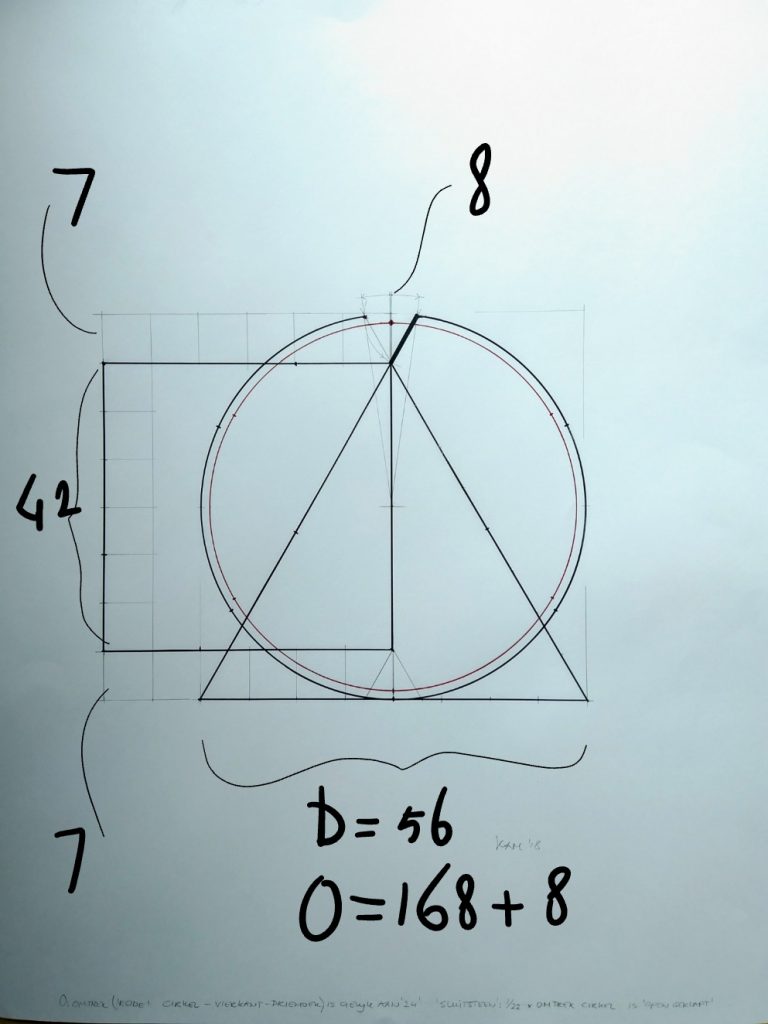
Op basis van graden én radialen
Eindoplossing als combinatie van de goede eigenschappen bij de vorige twee oplossingen.
De gekozen diameter is nu 7 * 8 = 56
Verdere berekeningen zijn af te leiden uit het bovenstaande.
Alle maten zijn gehele getallen en
dus goed toepasbaar in de praktijk van handwerkslieden.
NOTA BENE
Voor de fijneslijper , als we zeggen voor een cirkel:
‘de omtrek is 3 * 8‘
dan is dit feitelijk wiskundig geformuleerd onjuist.
Er is hierboven sprake van twee verschillende oplossingen.
– Voor de rode GESLOTEN cirkel geldt:
Pi ( ( 3 / Pi) * 8) , want rode ‘diameter’ is ( 3 / Pi) * 8
( dit betekent dat rode diameter ‘factor (21 / 22) kleiner is dan 8’ )
– Voor de zwarte OPEN cirkelboog geldt:
( Pi – (Pi -3)) * 8, want diameter is wel gelijk aan 8, maar er is een ‘opening’ aan de bovenzijde gelijk aan (Pi -3) * 8 = (1 /7 ) * 8