Wortel van 1 , ofwel decimaal getal 1,0000..
In (niet -repeterende) (niet-kettingbreuk) geheel getal te schrijven als
[ 1 ]
Toelichting over de ‘beweging’ van deze 7 vliegers.
Een vlieger is, behalve een reiziger op de strakke wind, ook een meetkundig figuur, namelijk een vierhoek met bepaalde bijzondere eigenschappen.
Ook het vierkant kan als vlieger worden geschouwd.
In dit geval past de vlieger zelfs binnen een ‘omgeschreven’ cirkel.
De verticale middellijn van onze vlieger splitst deze cirkel doormidden.
Als een symmetrielijn, links en rechts zijn identiek.
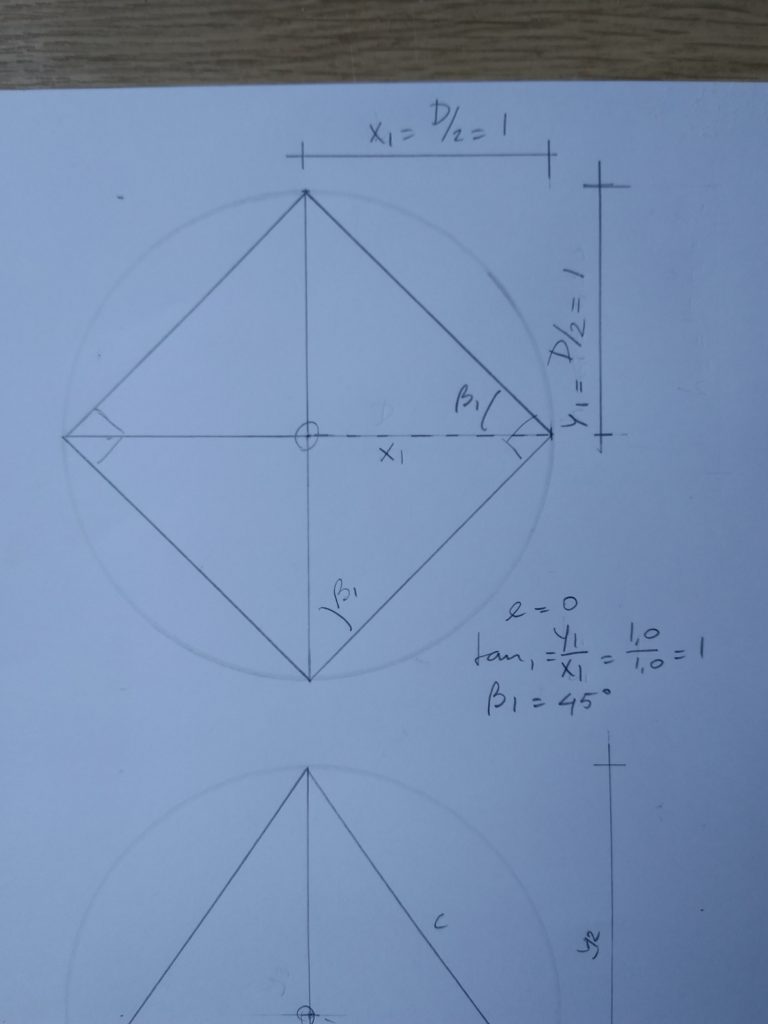
We beschouwen de zeven verschillende vliegers.
In het begin (donkerpaars) staat de horizontale loodlijn (horizon) in het midden.
Er is nu zelfs sprake van een dubbele symmetrie, links-rechts én onder-boven.
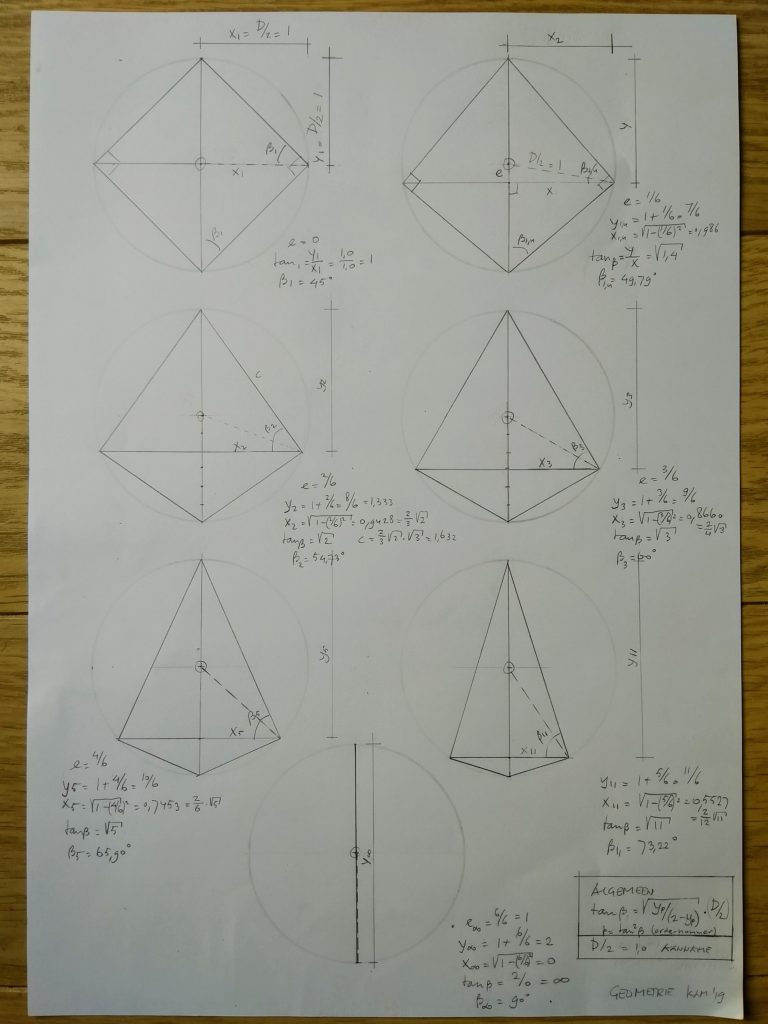
Bij de eerste stap (zie ‘hemelsblauw’) schuift de horizontale loodlijn (horizon) langs de middellijn een stukje naar beneden, in de richting van het laagste punt van de omringende cirkel.
Dat herhaalt hij daarna ( zie ‘frisgroen’) en elke stap is éénzesde deel van die afstand.
Meetkundig gezegd: e ( excentriciteit; minimaal 0 en maximaal 1) is de afstand tussen het middelpunt en de omringende cirkel, gemeten langs de middellijn, zogezegd de ‘weg’.
Grootte van elke stap is (1/6)n, dus e= ( 0; 1/6; 2/6; 3/6; 4/6; 5/6; 6/6 ).
In dat proces wordt die horizontale loodlijn ook steeds korter.
Totdat hij de cirkel raakt ( zie ‘stralend wit’) en uiteindelijk als een punt erin verdwijnt.
De vlieger is veranderd in de simpele verticale lijn die nu geheel samenvalt met de begeleidende middellijn.
De oppervlakte van de vlieger binnen de eenheidscirkel neemt steeds meer af, tot nul aan toe.
De oppervlakte is namelijk gelijk aan de hoogte ( die steeds hetzelfde blijft, het is de diameter van deze cirkel = 2) vermenigvuldigd met de lengte van de loodlijn ( dat is X; die begint als X = 1 en steeds kleiner wordt tot X =0)
De oppervlakte is dus maximaal 2 en minimaal 0.
En de tangens van schuine hoek (beta) , dat is de hoek van de horizontale lijn met de schuine zijde van de vlieger, wordt groter.
In stapjes van wortel ( 1, (7/5), 2, 3, 5, 11 tot ‘oneindig’).
Wat allemaal wonderbaarlijke getallen zijn, die als ‘eenvoudige’ repeterende kettingbreuk (In engels: continued fraction) kunnen worden beschreven.
Behalve de 1, het uitgangspunt, die repeteert zichzelf nooit.
Het gehele getal 1 moet als ondeelbaar worden beschouwd.
Zie voor meer toelichting over de verschillende wortels
ook de tekst in de gekleurde vakken.