Wortel van 2, ofwel: decimaal getal 1,4142..
In repeterende kettingbreuk te schrijven als
[ 1; 2]
Opmerkelijk zijn de overeenkomsten tussen de volgende drie vliegers ‘Pythagoras’, ‘Gulden snede’ en ‘Plastisch getal’.
Hun tangenshoek (lees hellingshoek) is bijna gelijk aan elkaar:
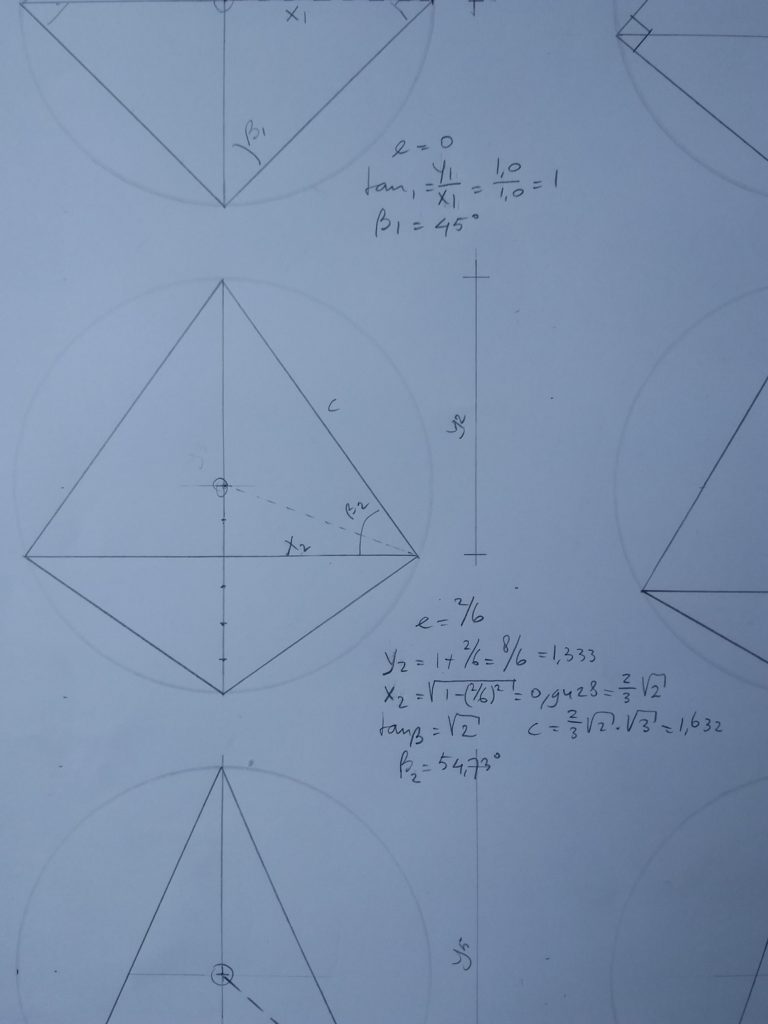
‘4/3 = 1,333’ , ‘wortel phi = 1,272’ en ‘psi = 1,3247’

Vlieger op basis van de bekende driehoek Pythagoras ‘3 – 4 – 5’

Vlieger op basis van Gulden snede getal ‘phi’ = {wortel (5)+1} /2

Vlieger op basis van ‘Plastisch getal psi’ = 1,3247…
zo genoemd door Dom van de Laan, architect
Toch zijn er ook verschillen, zoals blijkt uit de berekeningen:
-‘Pythagoras’ en ‘Plastisch getal’ kunnen ook door ‘eenvoudige’ breuk-getallen worden beschreven.
-‘Gulden snede’ kan worden geconstrueerd op grond van de opmerkelijke eigenschappen van zijn verhoudingsgetal ‘phi’.
-‘Gulden snede phi’ en ‘Plastisch getal psi’ zijn beide de oplossing van hun wiskundige formule ‘phi^2 – phi -1 =0’ en ‘psi^3 -psi -1=0’.
Ze zijn ook bekend door hun bijzondere maatreeksen van gehele getallen volgens Fibonacci en Padovan.