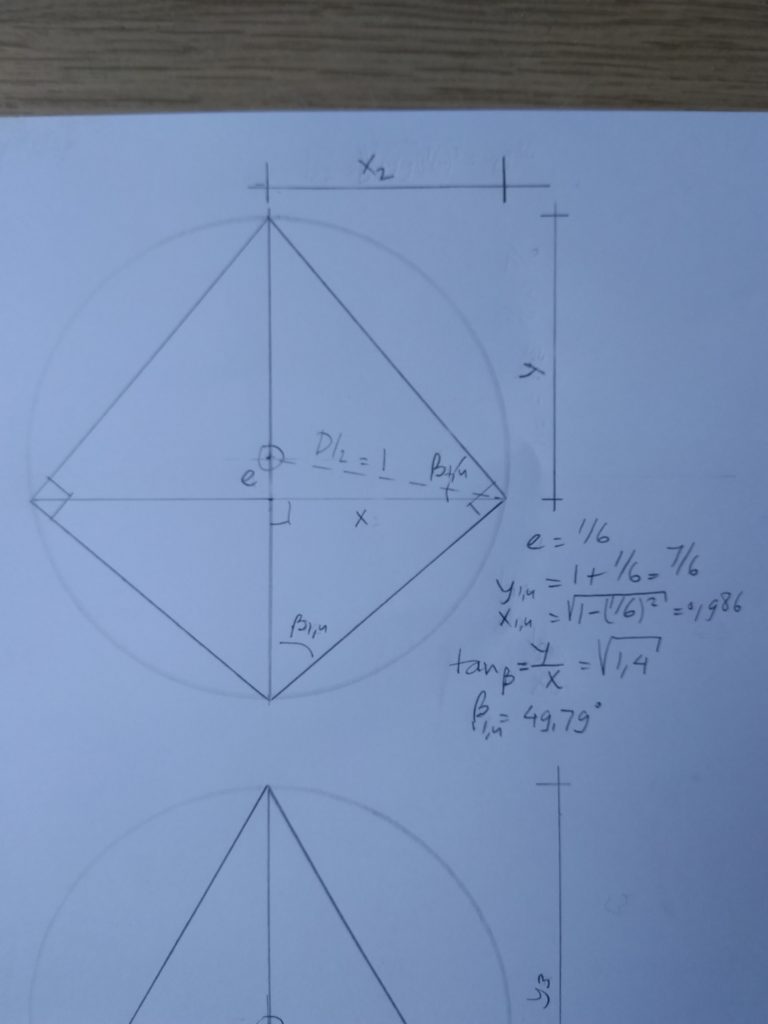
Wortel van 1,4 is gelijk aan wortel van 7/5,
ofwel decimaal getal 1,1832..
In repeterende kettingbreuk te schrijven als
[ 1; 5, 2 ]
Twee voorbeelden van bijzondere vliegers
met een omgeschreven cirkel.
Allebei de vliegers bezitten de ‘inwendige’ Pythagoras
driehoek 3 – 4 – 5, in het rood aangegeven als Basis driehoek.
De ene (1 – 2 – √ 5) heeft een hoogte- breedte verhouding
( lees: hellingshoek) van tan = 2
en de andere ( 1 – 3 – √ 10) van tan = 3.
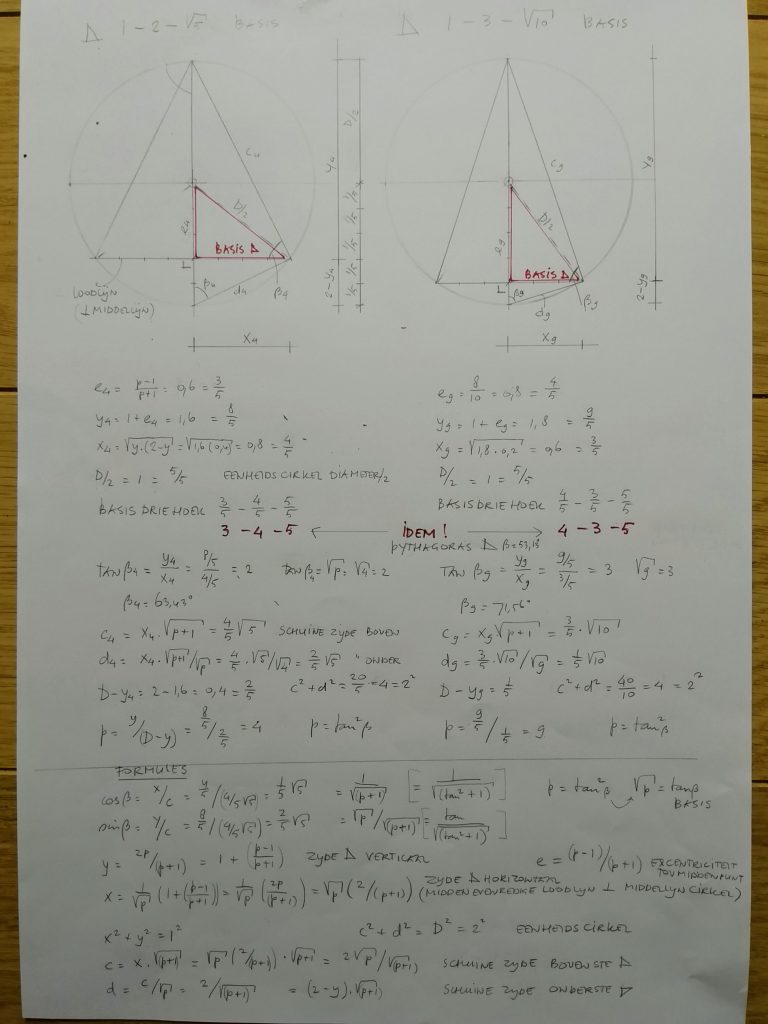
Hierboven zijn de basisformules gegeven.
Hiermee kunnen de maten van dit type vlieger op eenvoudige wijze worden bepaald, op grond van de ( tevoren als uitgangspunt gekozen) waarde van de ’tan (beta)’.
Tabel voor (tan^² ) >= 1, zie figuren hierboven (eenheidscirkel ‘basis’) voor de betekenis van de verschillende symbolen.
De, in de tabel berekende, waarde van e ( excentriciteit middelpunt cirkel ten opzichte van de horizontale loodlijn )
is zowel in decimale waarden en ( indien p een geheel getal is)
ook in zijn breuk-waarde te schrijven.
Bijvoorbeeld voor tan = 3:
tan^² ( tan-kwadraat) = 9
e = 0,80 = 8/10 ( = 4/5)
De ‘halve lengte van de loodlijn’ x = 0,60 = 3/5 ( = 2/10 √ 9)
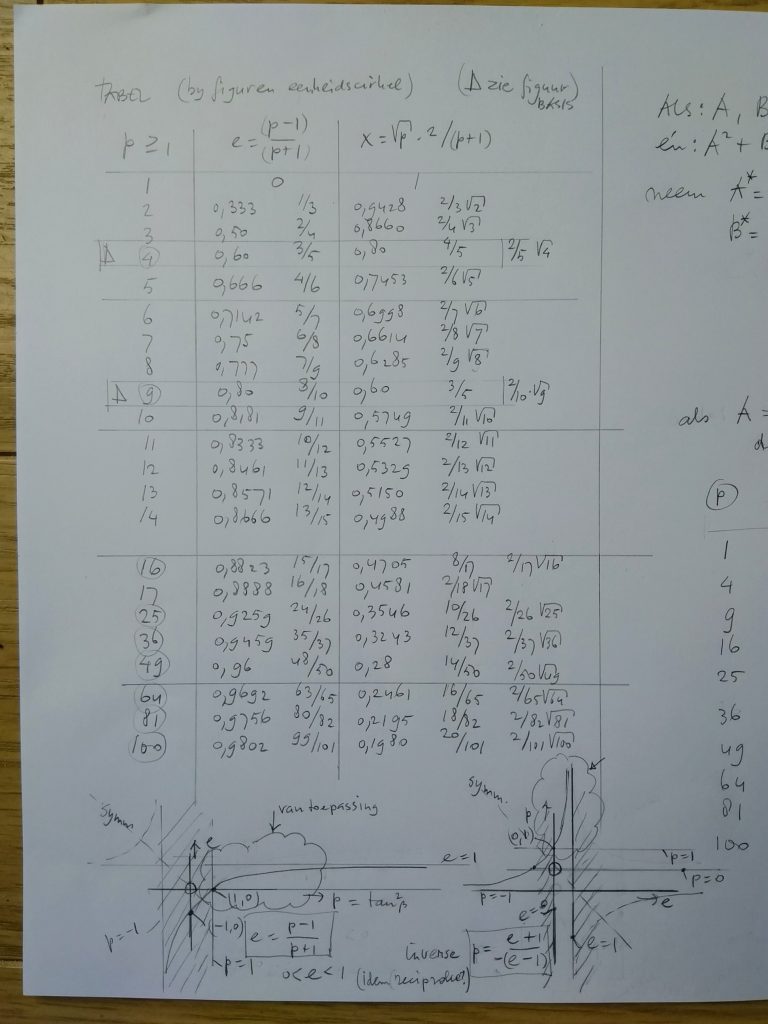
Als bijkomend voordeel kunnen nu ook bepaalde drietallen van een zogenaamde ‘Pythagoras driehoek’ eenvoudig worden afgeleid.
Stel dat de p = (tan^² ) zowel een kwadraat ( van een ander geheel getal) als zelf een geheel getal is. Dan kan met behulp van p de waarde van de zijden A – B – C van de driehoek worden bepaald.
Bijvoorbeeld als p = 4 dan:
A = 2 √ p = 2 * 2 = 4
B = p – 1 = 3
C = p + 1 = 5
