
Dit is de geometrie die volgens mij ten grondslag
ligt aan deze icoon.
Van oudsher heeft de mens steeds gezocht naar het meetkundige verband tussen de basisfiguren: de driehoek, het vierkant en de cirkel. Met name de omtrek van de cirkel is een groot vraagstuk.
We zien hier een een ( gele) cirkelboog, een ( rood) vierkant en een ( blauwe) gelijkzijdige driehoek. Op deze manier worden hier, denk ik, het hemelse/ geestelijke, het aardse/ materiële en de verbinding tussen beide symbolisch voorgesteld.
Wat hebben deze drie basisfiguren met elkaar gemeen?
Rondom gemeten ( langs de omtrek) hebben ze allemaal dezelfde lengte. Wat ons eraan wil herinneren dat er universele waarheden bestaan ( zoals 24 = 4 x 6 = 3 x 8) waaraan niet getornd kan worden. Hoe dat mogelijk is zal ik hieronder proberen uit te leggen.
Maar er is nog iets bijzonders aan de hand.
Misschien zag je het al.
De gele cirkelboog heeft een klepje aan de bovenzijde.
Het is dus geen gesloten, maar een open cirkel.
En die opening is net groot genoeg voor de duif om er doorheen te vliegen….
‘Het goede getal 12’
Waarom is 12 zo’n goed getal?

De waarde van breuken
Het getal 10 kan alleen worden gedeeld door 2 en 5;
Het getal 12 is echter deelbaar door 2, 3, 4 en 6.
Het jaar telt twaalf maanden, die ruwweg in vier seizoenen en twaalf tekens van de dierenriem zijn te verdelen.
De klok telt twaalf uren, die elk tweemaal per etmaal worden aangewezen.
Een dozijn als naam voor een twaalftal bestaat nog, maar een gros, een dozijn dozijnen, is bijna uitgestorven.
Het aantal graden in een volle cirkel is 360. De verdeling in 360 delen werd het eerst toegepast op de Dierenriem, ongetwijfeld doordat elk van de twaalf sterrenbeelden in dertig gelijke delen werd verdeeld.
Verdeling van cirkels in het algemeen in 360 graden werd het eerst toegepast door de Griekse astronoom Hipparchus, rond 130 voor Christus.
Bij benadering is 360 het aantal dagen in een jaar ( 365), ruwweg verdeeld in 12 maanden van elk 30 dagen.
Honderd jaar gelegen was het logisch om zeven eieren in een doos voor twaalf eieren te zien als 7 / 12 van de inhoud van de doos.
De moderne wiskunde geeft dan de voorkeur aan het decimale getal 0,5833.
Geen enkele oude beschaving zou 0,5833 hebben gebruikt voor zoiets simpels, zij hadden eenvoudige breuken. Die zijn beter te onthouden, gemakkelijker toe te passen en bezitten de exacte waarde die moet worden uitgedrukt.
Wat ik hier bedoel uit te leggen is, in plaats van te werken met een reeks cijfers achter de komma, kunnen bepaalde getallen, zoals twaalf, vrij goed worden opgedeeld met behulp van breuken, zoals 1/ 12 2/ 12 3/ 12 4 /12 enzovoorts.
Redenerend op dezelfde manier nemen we hier
ook eenvoudige breuken aan voor
Verhoudingsgetal Pi : breuk 22/ 7
Wortel (3) : breuk 7/ 4

Toelichting met behulp van geometrie -tekening hieronder.
De GESLOTEN inwendige cirkel is rood.
De OPEN cirkelboog ( aan de buitenzijde) is hier in het zwart aangegeven. ( Op de icoon is hij rood getekend)
Let op: De gesloten cirkel en de open cirkelboog hebben wél dezelfde lengte/ omtrek!
Beloofde eenvoudige uitleg:
als bij een metalen hoepel is de rode GESLOTEN cirkel aan de bovenzijde doorgezaagd.
Vervolgens is deze hoepel daar een stukje OPENgebogen.
De in de opening passende zwarte ‘sluitsteen’ ( als aanwezig bovenin gewelven in oude gebouwen) ligt ( naar beneden, hier dubbeldik aangegeven) schuin tegen de hoepel aan, naar beneden geklapt en staat dus open.
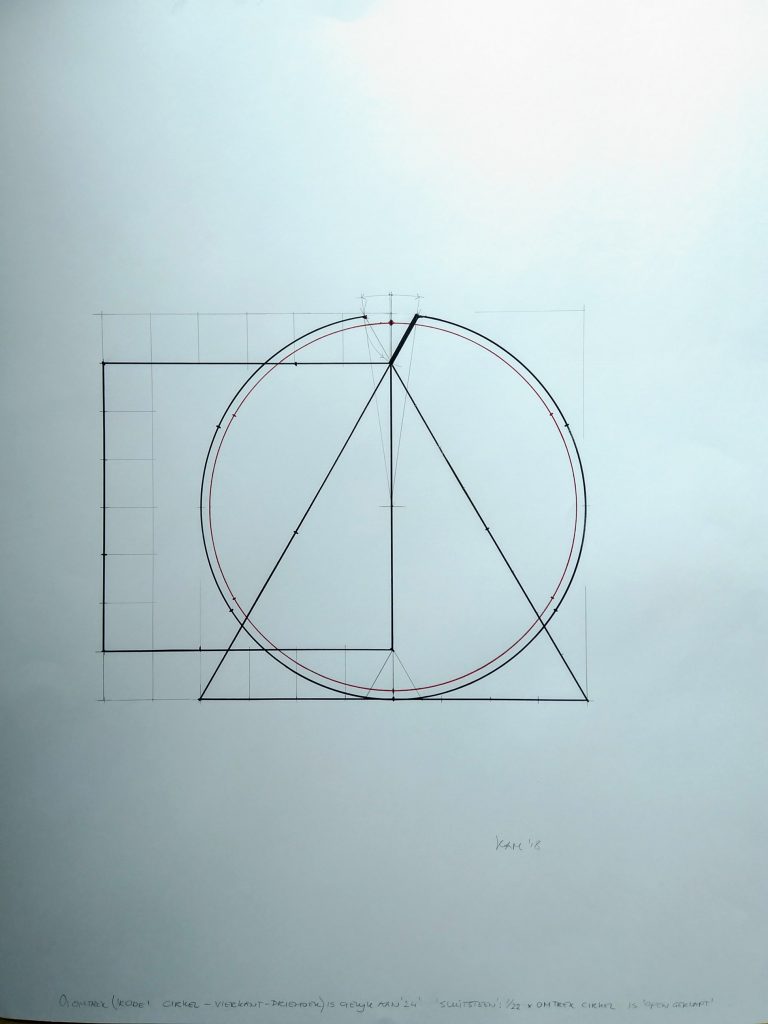
Praktisch voorbeeld voor berekening omtrek cirkel
De Babyloniërs ( 2000 v. Chr.) stelden: de omtrek van een cirkel bedraagt hetzij 3, hetzij 3 1/8 maal de diameter.
Ruwe maar praktische benaderingen voor handwerkslieden of technici. Het gebruik van een lang touw met knopen (meetsnoer) was een gebruikelijke methode om maten uit te zetten.
( Bijvoorbeeld met behulp van de rechthoekige driehoek 3 – 4 – 5.)
Circa 960 voor Christus, ten tijde van de bouw van de tempel van Salomo, kan uit deze tekst in het Oude Testament worden afgeleid dat de omtrek van een cirkel vroeger gelijk was aan
” 3 maal zijn ‘diameter'” was, zie 1.Koningen 7;23
Verder maakte hij de gegotene zee;
van tien ellen was zij van haar enen rand tot haar anderen rand, rondom rond,
en van vijf ellen in haar hoogte,
en een meetsnoer van dertig ellen omving ze rondom.
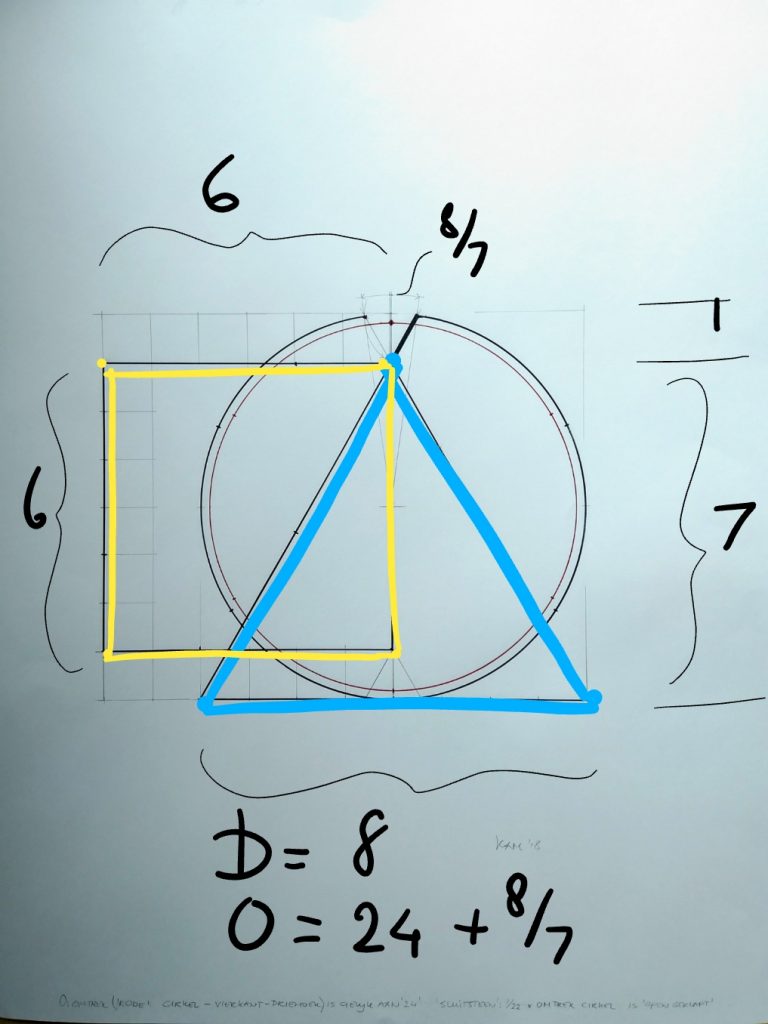
We gaan op basis van de tekst uit 1.Koningen de omtrek van de cirkel – driehoek – vierkant berekenen.
– Omtrek rode gesloten cirkel is 3 * 8 = 24 ( naar Salomo, zie boven)
want gekozen ‘diameter’ ( ‘van ene rand tot andere rand’) is hier gelijk aan 8 gekozen ( ongeacht de maateenheid/ meters/ ellen)
zodat de omtrek 24 in ieder geval een veelvoud van 12 is.
Daaruit volgt
– Omtrek blauwe driehoek is ook 24 , dus zijde 24 / 3 = 8
– Omtrek gele vierkant is ook 24, dus zijde is 24 / 4= 6
Daarbij nemen we eenvoudige breuken aan voor
Pi : breuk 22/ 7
Wortel (3) : breuk 7/ 4
Zodat bij blauwe driehoek is verhouding ‘hoogte/ breedte’ gelijk is aan: 7 /8
Omtrek van zwarte open cirkelboog is ook 24
De ‘resterende’ opening aan de bovenzijde is (ook hier dezelfde driehoek in klein formaat)
(Pi – 3) * 8 = (( 22 / 7) – (21 / 7) ) * 8 = ( 1/ 7) * 8 = 8/ 7
Zie hierboven het resultaat, de geometrie waarbij de drie basisfiguren met elkaar zijn verweven
op een onderliggend eenheidsraster
Nota bene: dat het ‘gele’ vierkant op de icoon naar het midden is verschoven, is irrelevant. Hetgeen wordt aangetoond ( gelijke omtrekken) in deze geometrie blijft ongewijzigd.