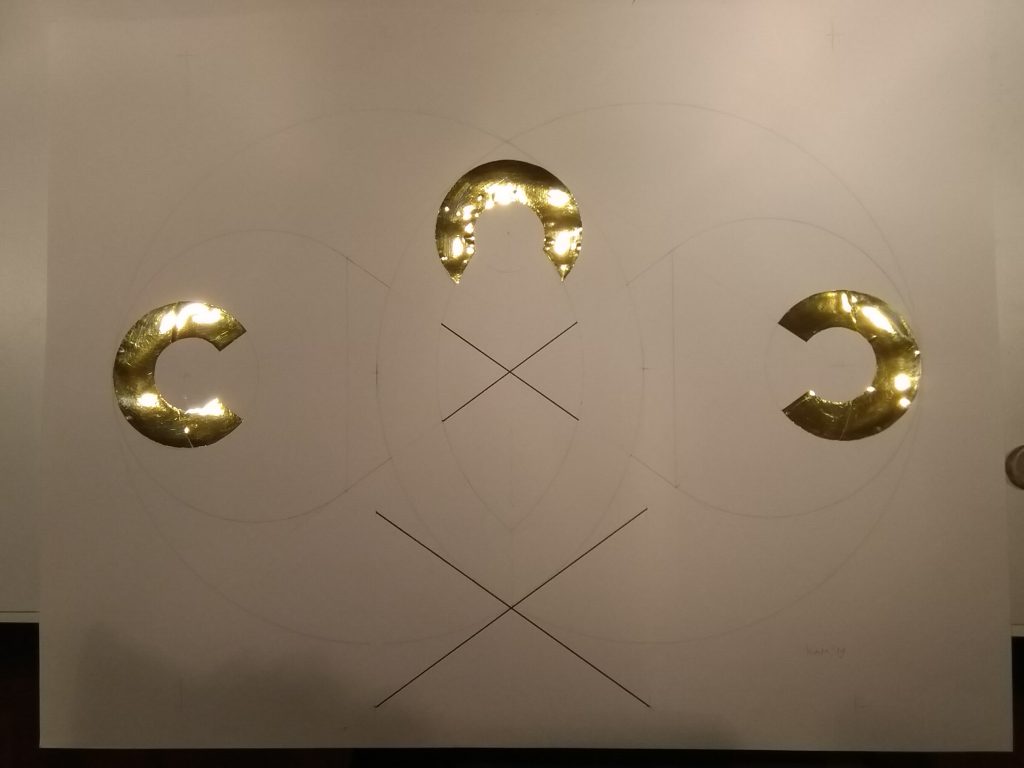
De originele, bovenstaande tekening stond binnen een uurtje op papier. Hij is eenvoudig van opzet, gewoon een paar lijnen en wat cirkels.
Wat kan daar nu moeilijk aan zijn?
Maar eerlijkheid gebiedt mij om te zeggen dat het me daarna nog drie volle dagen kostte om de onderliggende structuur ervan te achterhalen.
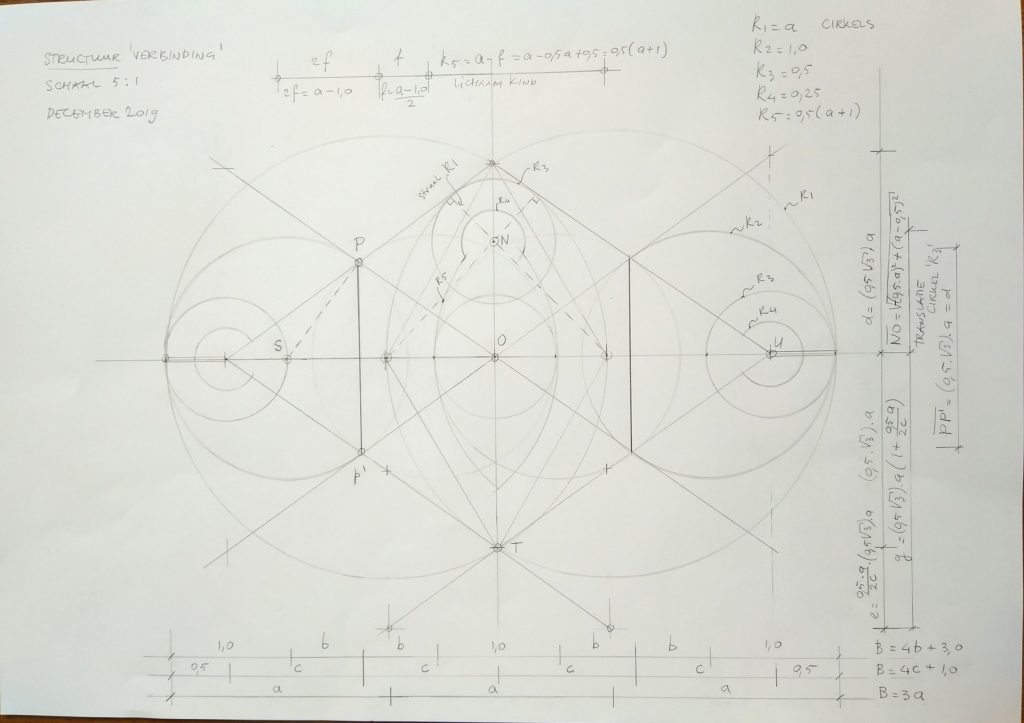
En die structuur, dus deze meetkundige figuur, had ik echt nodig vóórdat ik de tekening kon gaan omzetten naar zijn digitale ( met computer getekende) versie. Ten behoeve van het drukwerk van de kerstkaart voor Augustinus Eindhoven.
Het waren drie bijzondere dagen. Er was zoveel te ontdekken.
Dat had ik van tevoren niet verwacht!
Tegelijkertijd waren er in elke nieuwe figuur weer symbolische eigenschappen te vinden ( die op de voorpagina duidelijker gemaakt worden.) Maar laten we beginnen bij het begin.
Dit is de icoon zoals hij op de kaart staat:
Icoon kerststal ‘Verbinding’
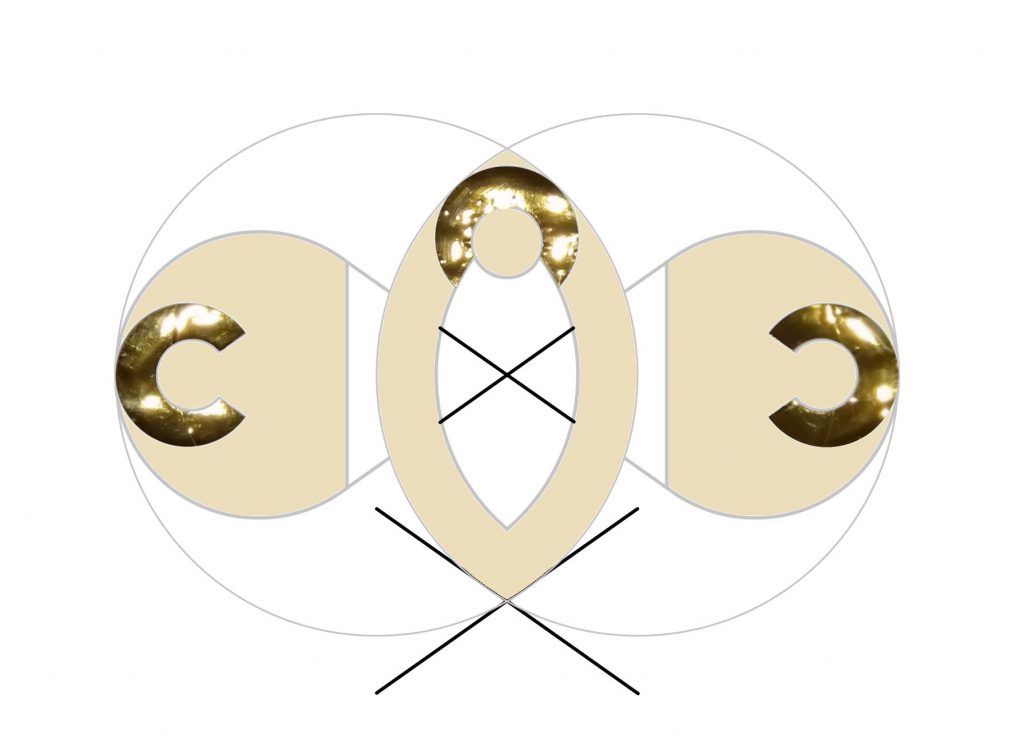
Wat je ziet zijn wat in elkaar gevlochten cirkels en lijnen.
En dat is ook juist.
Maar eigenlijk zijn het meerdere figuren, die samen één geheel vormen.
Dat wil ik je graag met wat plaatjes uitleggen.
Maar eerst wil ik je verrassen met een prachtige gelijkenis.
Cellen vermenigvuldigen, kerndeling of mitose (Wikipedia)
onder microscoop, filmopname
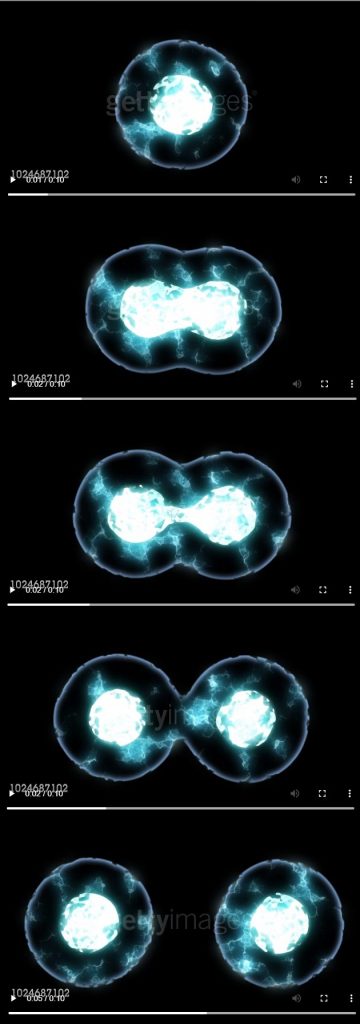
Celdeling vind ik het grootste wonder van het leven.
Uit één moedercel ontstaan, door deze drang tot splitsing, twee identieke dochtercellen.
Iets dat steeds maar doorgaat, ongemerkt en onafgebroken.
Dat er enorme krachten, in combinatie met grote nauwkeurigheid, bij komen kijken, heeft men pas kortgeleden ontdekt.
Waar doen je deze vormen aan denken?
Juist ja!
Twee cirkels die elkaar gedeeltelijk overlappen

“De kern splitst zich in tweeën.”

“De nieuwe kernen laten elkaar los, de kerndeling is gereed.”
Zoals je ziet heb ik alvast wat maten erbij gezet.
Getal 1 is hier de basis- referentiemaat, dit is het uitgangspunt.
De tweede maat is een ‘nog onbekende’ waarde,
hier aangegeven als ‘φ’ ( spreek uit als ‘fi’).
Tweemaal: ’twee cirkels die elkaar gedeeltelijk overlappen’
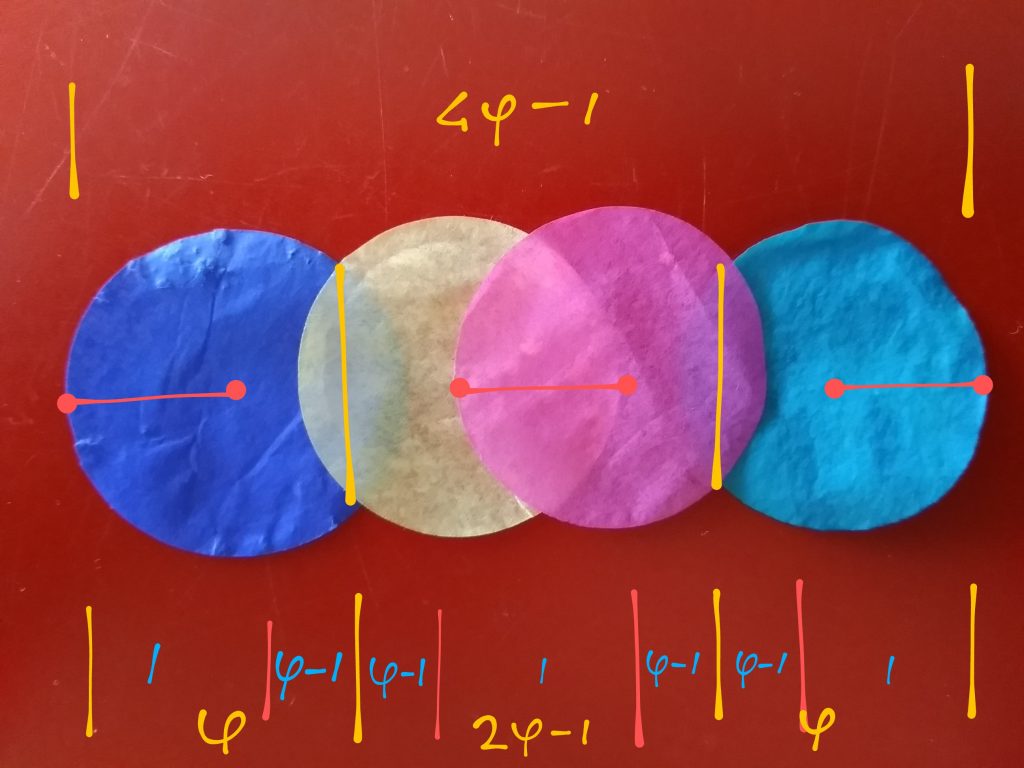
Er zijn drie maten ‘1’ te vinden.
De totale breedte ( dit is een belangrijke maat) bedraagt: 4 φ -1
Vier cirkels op een rij.
Hier herken je vast weer de twee kernen van het tweede plaatje.
Ze staan in het midden. Deze cirkels overlappen elkaar voor de helft.
En je ziet ( links én rechts ) ook de twee kernen van het derde plaatje. Die zijn namelijk nét iets verder uit elkaar geschoven.
Samen vormen ze dus één geheel, met alleen die typische maten ‘1’ en ‘φ’ .
Nu ken je de basis van de meetkundige structuur.
Valt nog best mee, toch?
Je kunt het hierbij laten of nog wat verder lezen, wat je wilt.
Op zoek naar oplossing gaan we alle maten uitdrukken in ‘φ’.
Gezien de cirkel een straal 1 heeft,
is ‘φ’ dus groter dan 1 en kleiner dan 2.
De sleutel binnen deze icoon is te vinden in de oplossing
voor de nu ‘nog onbekende’ waarde ‘φ’.
Daar gaan we dus naar op zoek.
Maat a volgt uit: de twee grotere cirkels

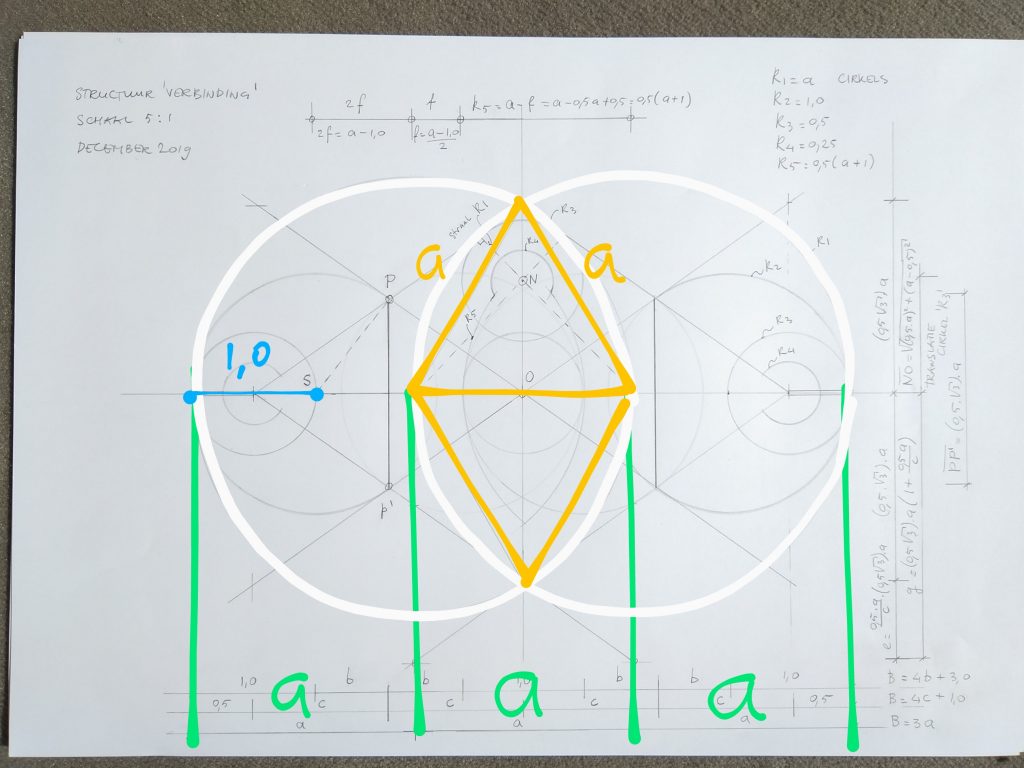
Deze vorm heet de Vesica Piscis.
Zie hierboven “Vier cirkels op een rij”
de totale breedte is 4 φ -1
Dus hier geldt 3a = 4 φ -1
Ofwel a = ( 4 φ -1 ) / 3
Maat b volgt uit: de drie kleinere cirkels ‘1’
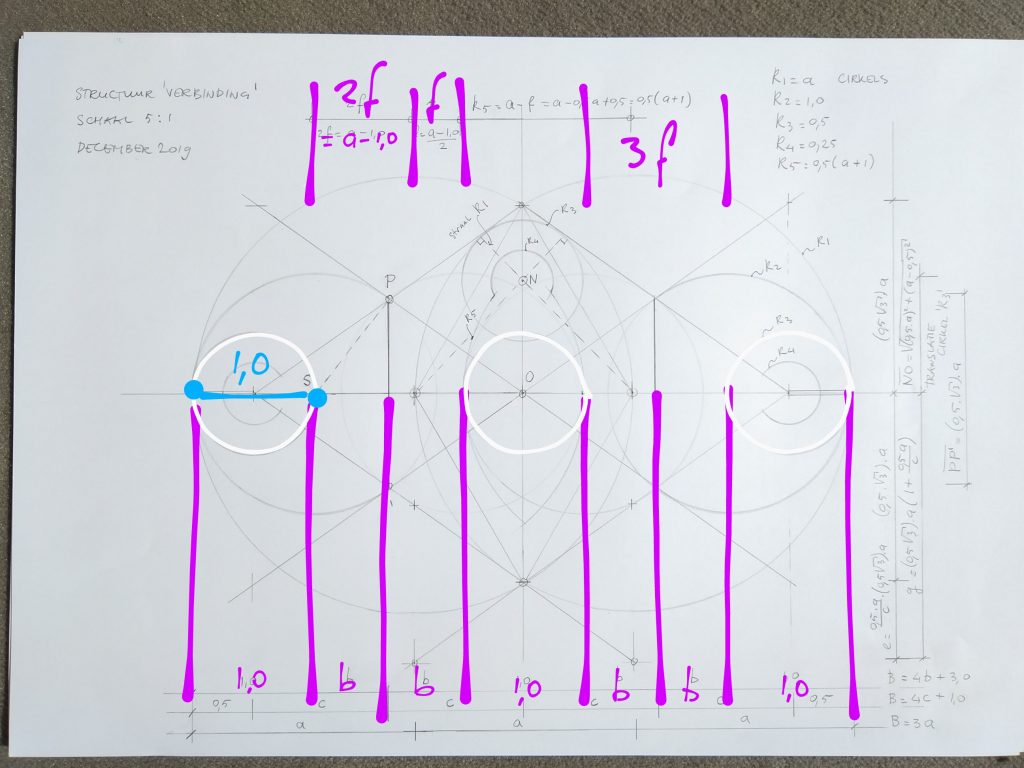
en tegelijkertijd zien we dat
maat f = ( a – 1) /2 = 2b /3 = 2 ( φ -1) /3
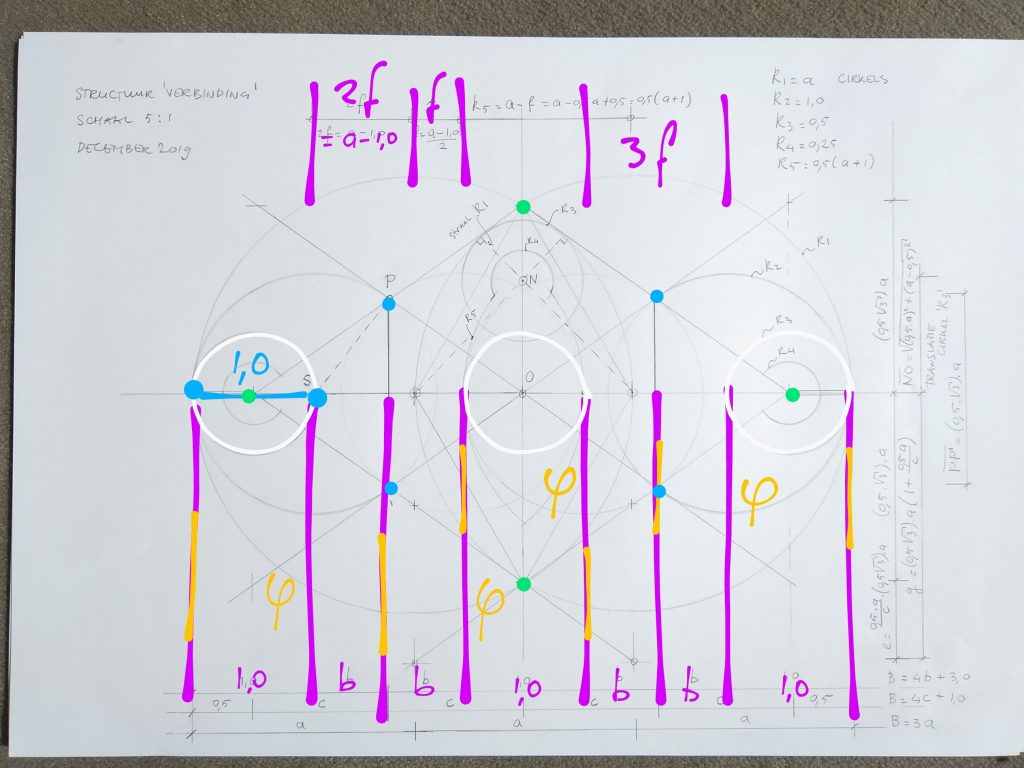
Maten c en d volgen uit: de vier “kern” cirkels op een rij

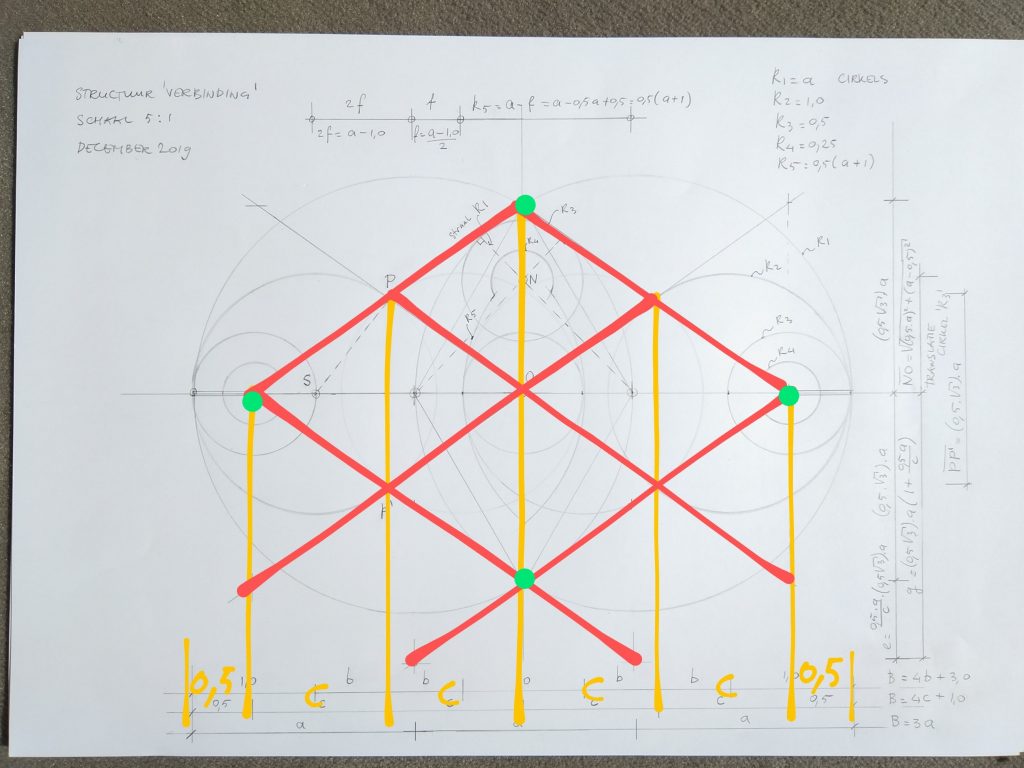
Het (rode) schuine raster gaat door de ‘groene’ punten.
Dit zijn de belangrijkste punten in de geometrie.
De horizontale verdeling is gelijk aan de maat c.
De verticale verdeling aan maat d.
Op de icoon zie je het raster plaatselijk als een X terugkomen.
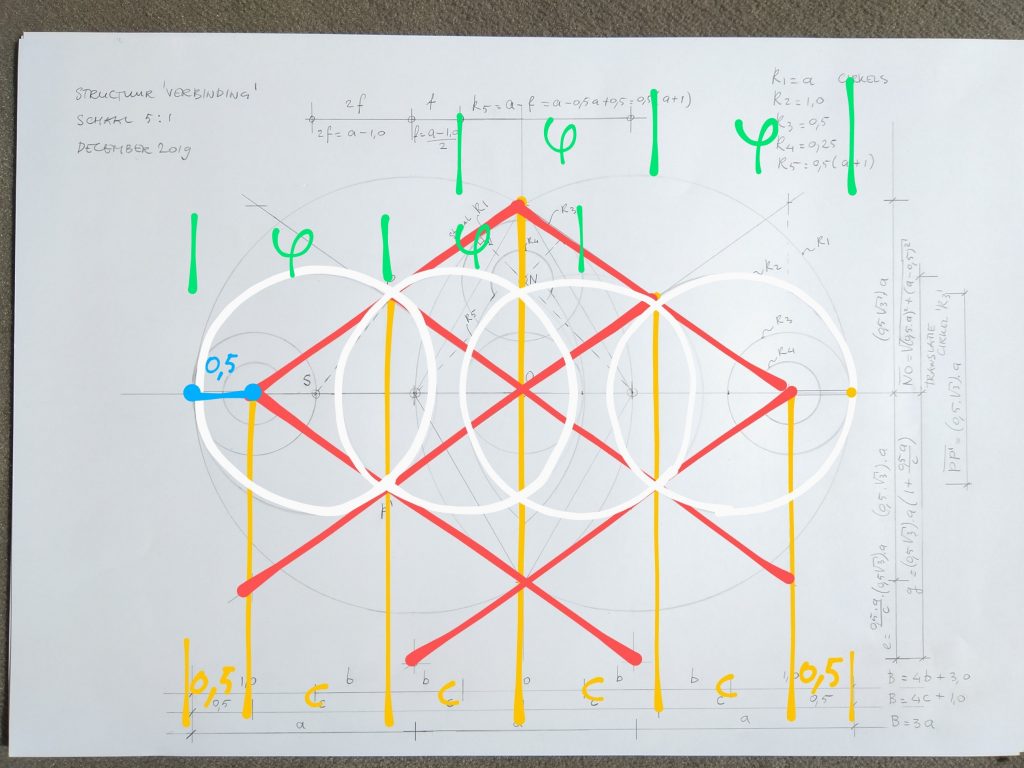
Horizontale maat c = φ – 0,5
en
Verticale maat d = 0,5 wortel(3) . a
= 0,5 wortel(3) . ( 4 φ -1 ) / 3
Belangrijk uitgangspunt is oneindigheid
Het oneindigheids- symbool ( de liggende 8 ) moet naadloos kunnen doorlopen, dus van de cirkel links over de schuine lijn naar de cirkel rechts en over de andere lijn weer terug.
Want exact ter plaatse het blauwe punt P
zit de aansluiting tussen de twee witte cirkels en het rode raster.
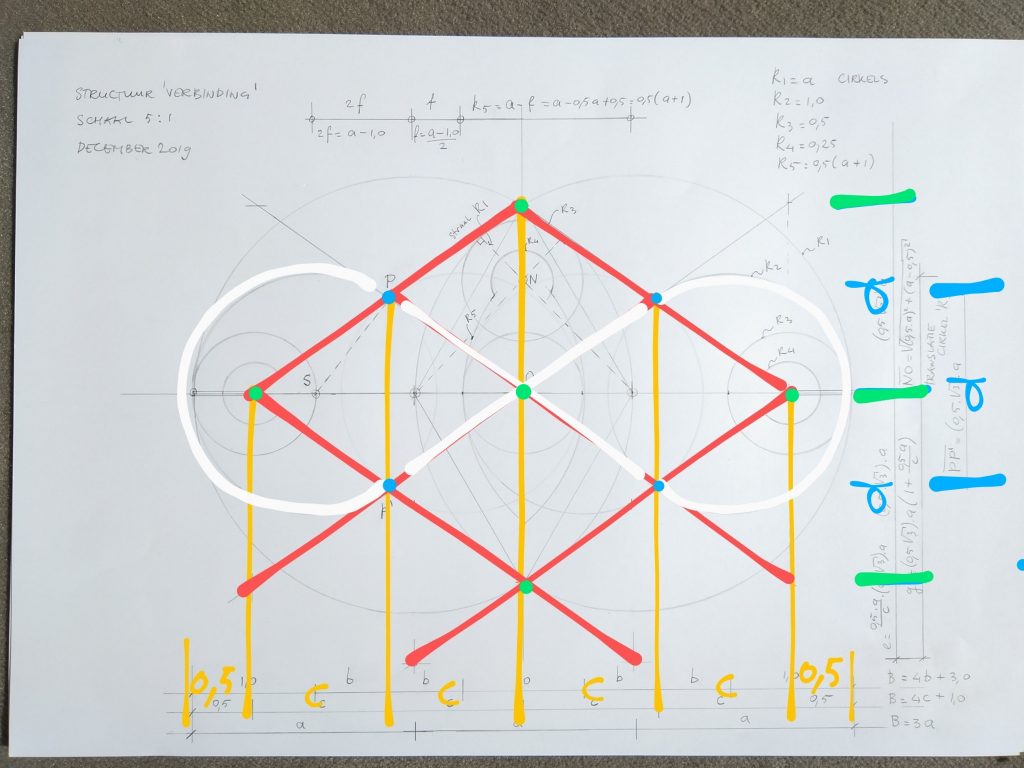
Aansluiting van buitenste witte ‘kern’ cirkels op het rode raster
in de vier blauwe punten P
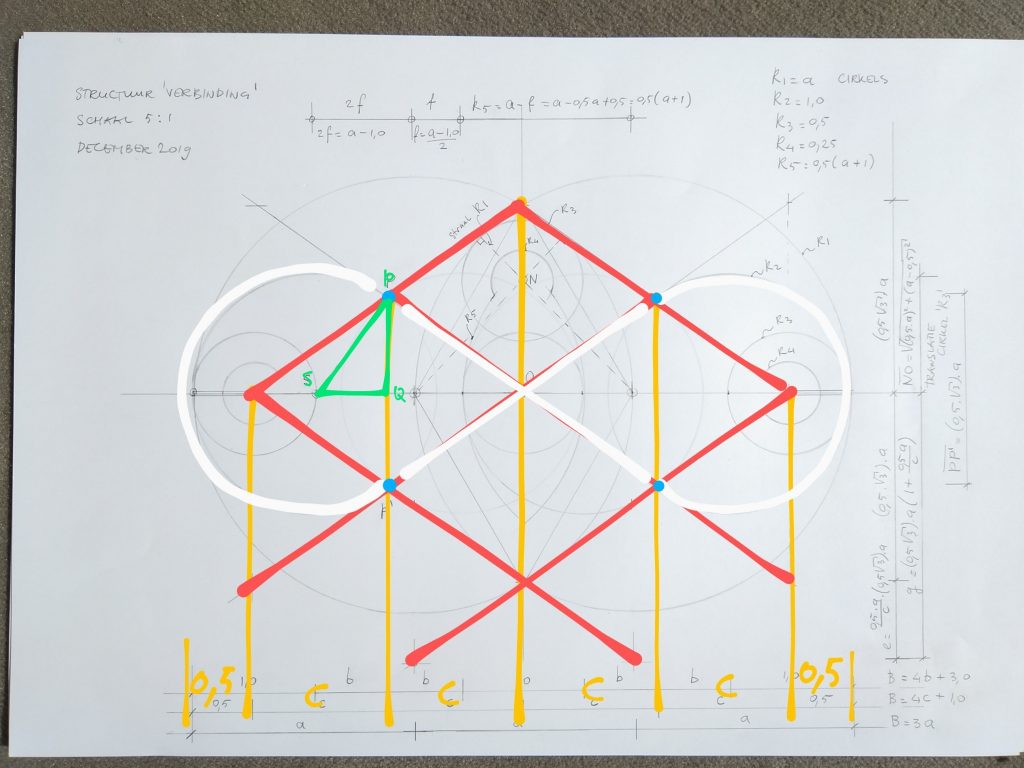
De groene rechthoekige driehoek zorgt voor de oplossing.
De vergelijking voor de lengte van de zijden van deze driehoek is
SP^2 = SQ^2 + PQ^2
met
SP = 1 straal van de eenheidscirkel
SQ = b = φ -1 horizontale maat
PQ = 0,5 d = 0,25 wortel(3) . ( 4 φ -1 ) / 3
Zie hieronder de vergelijking

is de oplossing van de vergelijking met de ‘onbekende waarde’ φ .
Zie deze berekening.

volgens mijn calculator
als bewijsstuk
Eindresultaat
Omdat de waarde van φ bekend is, kunnen nu ook alle andere waarden van a tot en met g worden berekend. Zie hierboven, de handgeschreven berekening.
Te beginnen met
a = 1,82043
b = 0,6153 en f = 0,4102
c = 1,1153
d = 1,5765
e = ( 0,5 a / 2 c) d = 0,6433 poot kribbe verticaal
g = d + e = 2,2198
en dus is de totale breedte = 5,46130
De tekening van de geometrische structuur kan daarmee op schaal worden getekend.
Jammer voor degene ( mijzelf incluis) die hier had verwacht dat de oplossing van φ gelijk zou zijn aan het getal van Fibonacci ( gulden snedegetal) Fib = (wortel (5) + 1 ) / 2 = 1,618033.
Want dan zou deze ‘groene rechthoekige driehoek’ een “Driehoek van Kepler” zijn.
Wikipedia: Driehoek van Kepler
Fib – 1 – Wortel(Fib) = 1,618 – 1 – 1,272
( Hoek 51,8 graden)
Bij ‘groene driehoek’, lengte zijden zijn (waarden ter vergelijking)
1- b – 0,5d = ( 1 – 0,615 – 0,788 ) /0,615 = 1,625 – 1 – 1,281
( Hoek 52,0 graden)
Maar met het blote oog is het verschil echt niet te onderscheiden.
Verhoudingsgewijs Fib / φ = 1,6180 / 1,6153 = 1,0016
Nota bene.

Enne… als je misschien nog op zoek bent naar het Wagenwiel:
dat zit ter plaatse van punt O in het midden.
Titel kerstkaart
De titel “Het Kind in de kribbe verbindt zijn Vader en Moeder in eeuwigheid” is voor meerderlei uitleg vatbaar.
Een kind dat geboren wordt, maakt van de beide ouders ‘zijn vader en moeder’. En op hun beurt deden die ouders dat als kind weer bij hún ouders. De familieband vormt een essentieel onderdeel van het mens-zijn.
Dit Kind is Jezus, aan zijn wiegje in de kerststal zitten hier Jozef en Maria.
Het is dezelfde Jezus die God als zijn Vader kent en Maria als zijn moeder. Maria, die moeder mag zijn van alle mensenkinderen.
In wezen verbindt Hij God, zijn Vader, met ons allemaal.
In eeuwigheid, dat is nog het allermooiste.
Inspiratie voor tekening kerstkaart, icoon Anastasis
De icoon ‘Anastasis’ is de inspiratiebron voor deze tekening van de kerstkaart “Verbinding”. Een verhaal op zich, dat je vast wilt horen.
Hier kun je lezen hoe dat in zijn werk ging.